Have you decided at what age you’ll start drawing on social security? The income insurance plan will let you choose to do so between ages 62 and 70, with increasing benefit amounts the longer you wait. Have you thought about taking social security at 62? In this post, I’ll review the pros and cons behind taking social security early and waiting. We’ll look at what it’d take to beat the age-related increases by investing the disbursement amounts beginning at age 62 as well.
Social Security Retirement Planning
I’m writing to you today from my first Amtrak ride since the pandemic started. The train is trundling along, heading north along the eastern coast on its way to the northeastern corner of the US. We’re passing through the tiny railroad town of Ashland now.
I’m on this ride in order to reach my father who is having knee surgery tomorrow. He needed someone available to cart him back from the hospital. It’s also a good excuse to get some father-son time. By the time this is published, the surgery will be complete, and (hopefully) he’ll be on the road to recovery and a brisk pace once again [update: the surgery went well!].
While I was planning the trip with him over the phone last week, he offhandedly mentioned that he and my mother were working through some retirement plans (for the nth time).
As is often the case, I tried to get my bearings for what they were planning to do by asking high-level questions before he got too deep into the weeds.
They’re both now in their 60s and trying to seriously plan an exit from work and onto retired life. My dad suggested their timeline would be “Spring 2023”—so about two years off.
I asked what their motivation was for that particular time period. While the answer involved multiple concerns, including completing some home improvements in preparation to sell, one key point was related to social security.
Social security benefits by age
I have a decent grasp of how the US social security system works. But I don’t have a great understanding of some of the details on how your monthly social security check is calculated.
My parents want to wait until later breakpoints within the social security system to earn the greatest benefits.
For example, at one age, say, 62 they might earn $1,000 per month if they start drawing on it at that age. However, they could opt to wait until a later age. Perhaps they wait until 67 and they earn more monthly benefits—maybe $1,400/month.
Side note: the average monthly social security benefit for 2020 was $1,543 per retired worker (per the SSA).
But, in my head, this doesn’t seem like a great deal on the face of it. I’d think that the total social security benefit is largely based on actuarial tables and the time period they can draw the benefit.
Meaning, if you draw $1,000/month from age 62 to death (let’s say 80 years old), your total benefit would be similar if you start drawing at age 67 even if it’s more money per month.
I didn’t have much to back up this idea during the conversation with my father aside from a vague sense of how social security works.
So, today, I wanted to work through these numbers with you so that I have a more definitive explanation for my parents. As you might guess, I’ve encouraged them to consider cutting loose and enjoying what remains of their lives, especially the small things, sooner rather than later.
If one of their motivations to wait is to draw a larger social security check, but the underlying math doesn’t really support that as a financially smart decision, I want to tell them that.
Similarly, I want to be able to help you understand the system better. Not only for your own elderly family and friends but also for yourself.
While many of us within the FIRE community frequently don’t include social security within our retirement calculations, I think it’s constructive to understand how the system works and how you might best make use of it. Even if you’re not considering taking social security at 62, that doesn’t mean you shouldn’t understand the implications.
That’s if social security still works similarly as it does today once you actually reach the appropriate age!
How does the system work?
These are the questions I have:
- How are social security benefits calculated? This is a basic question, and my current impression is that it’s based on a period of your highest-earning years. I believe it’s your top thirty years, but I want to confirm that [update: it’s 35 years!]. Assuming it is only a certain period (and not your entire working life), for many people, they’ll reach their max around age 56 if they work a continuous 35 years after typical college graduation.
- What’s the best age to start collecting social security? I’m wondering this from the perspective of a frugal investor. In other words, my comparison between drawing at one particular age—say, 62–and another—perhaps 67–isn’t just the net benefit amount before death. It’s also considering that the benefit for the five extra years in the younger scenario would be invested (however conservatively) and produce some growth over that period.
- How are SSA benefits treated in terms of taxes? If they’re treated simply as another income source like a W2 or 1099, it’ll be important to figure in this income when working out tax strategies in terms of realizing investment growth and capital gains.
Now that the research has begun… Here are some key stats:
- Starting benefit age range: anytime from age 62 to 70
- Based upon your 35 highest-earning years
- Historical earnings years are indexed to retirement year dollar values (e.g. your $15,000 salary in 1960 adds more to your benefit than the same $15,000 salary in 2021)
- “Bend points” mean your benefit amount is progressive; you get more out of lower wages than higher
- Benefit amount is typically adjusted with CPI (inflation) annually
- Benefits are subject to income taxes in a similar way as any other income with some mild caps/deductions at very low-income levels (mostly for those that live on only social security)
Social security retirement age chart
The age you choose to begin receiving your social security benefit significantly impacts the benefit amount.
Here’s an example from the Social Security Administration (SSA). Below is a social security retirement age chart from some of their documentation:
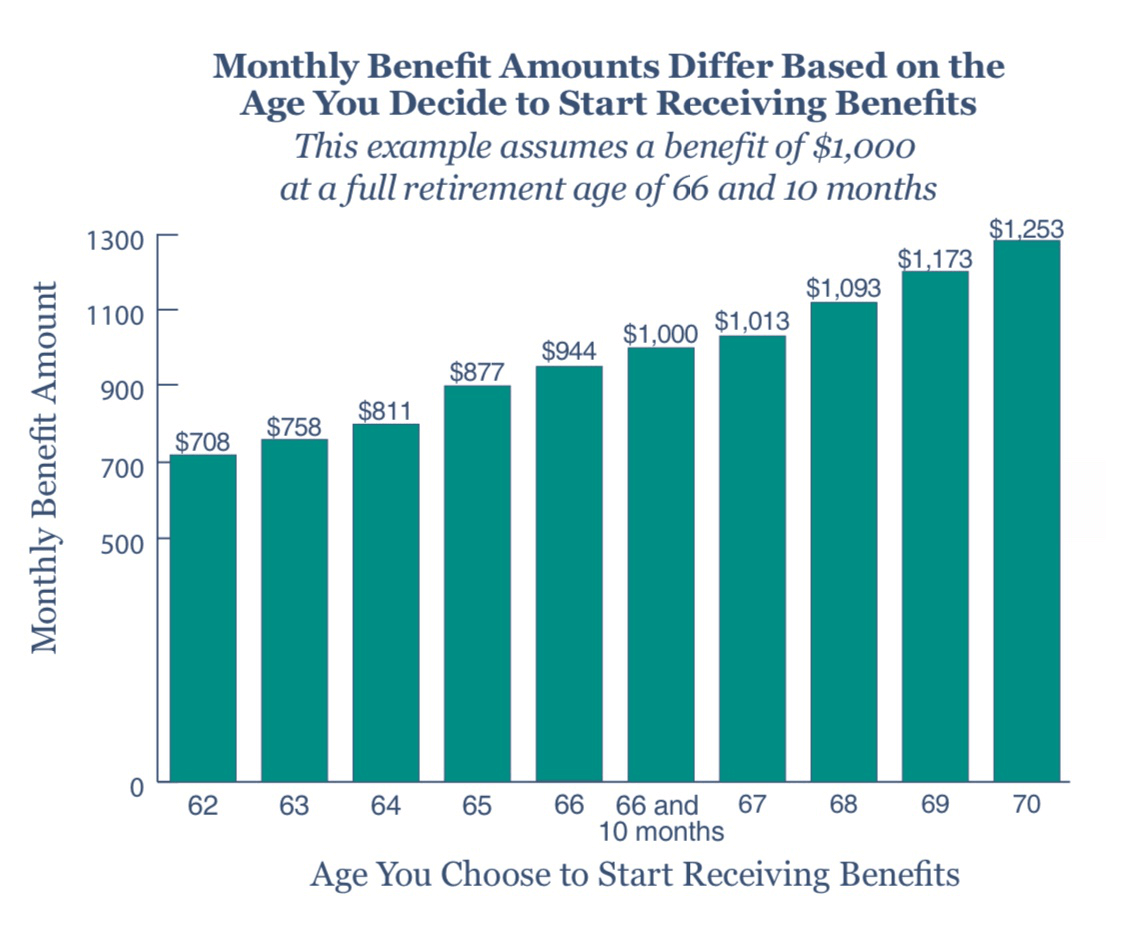
Looking at the chart above from the SSA, the very first question that springs to mind is this. Could you expect to conservatively invest $708/month for a 58 month period (age 62 to 66 and 10 months) such that it’ll make up for the earnings difference?
In other words, if you choose the $708/month at age 62 benefit, you’ll earn $292 ($1000 minus $708) less per month from age 66 and 10 months onwards. Is it possible to take the earnings, invest them conservatively (not in stock picking!), and expect to produce $292/month in appreciation and dividends moving forward?
If the answer is yes, then it seems like it may make good financial sense to invest the proceeds starting at age 62 if your plan was to wait until “full retirement” at age 66 and 10 months. At that point, you’d still produce $1,000/month through the benefit and investment return yet still have the original principle earned from age 62 through full retirement age.
First, let’s calculate the earnings we could invest from.
We know there are 58 months earned at $708/month from age 62 to “full retirement” in this scenario. That’s $41,064 in benefits paid over that period.
Presumably, we’d start investing the benefit value immediately. But let’s run an easier calculation that’s less advantageous.
Using the simple 4% rule, what could we expect to safely draw from a $41,064 investment? The answer is $136.88 per month.
That only gets us to about 47% of our $292/month goal!
More realistically, we’d conservatively invest each $708/month benefit.
What about investing the monthly benefit?
Let’s see what that’d look like when considering typical appreciation and dividends over a 58 month period (rather than holding it in an account that earns nothing over that time).
If we expect our monthly $708 investment to earn about 6% when including dividends, our investment should be worth about $47,600 after 58 months. That’s an improvement of about $6.5K. Nothing to sneeze at. But it’s not going to more than double how much we can safely withdraw.
At this point, it sure looks like my idea is bunk. Dead in the water. Everyone should wait until full retirement age to start drawing from social security.
But wait. Is that really so?
We’re missing a pretty key component to the calculation so far.
And that is, to put it grimly, how long you expect to live.
Social security and longevity
SSA provides a great, simple longevity calculator to help you figure out how long your benefit will last (along with your life). This calculation is different from life expectancy.
For example, life expectancy in the US is a bit over 78 years. But that includes all the unfortunate souls that die young. If you’re already, say, 60 years old, you’ve avoided those early life pitfalls and will have an expected death later than the overall life expectancy.
For example, for my father, the SSA calculates his longevity as 84.4 years. My mom is a bit younger and so her estimate is 86.0 years.
As a point of reference, the SSA suggests I’ll kick the bucket at 81.7 years. My longevity is actually less than theirs (though greater than the US average) because I haven’t yet survived through the time period that they have.
Spending down your invested principle
Going back to our SSA benefit calculation, we don’t need our $41K or $48K to last for 30 years or so like the 4% rule was set up for.
In fact, if our intention is to compare the choices of picking the benefit at age 66.8 or 62.0 and waiting to drawdown until 66.8, we know that in either circumstance we should aim to drain the account by age 84.4 (for my dad). That’s just a 17.6 year period.
In fact, simply taking our nest egg amount of $41,064 (the total if we didn’t invest our benefit starting at age 62) and dividing it over 17.6 years will yield a monthly value of $194.43.
If we were to work from the amount we calculated where we invest the monthly benefit up until age 66.8 ($47,600), that yields a monthly value of $225.38. That’s much closer to our $292 goal, but we’re still quite short.
In the final piece of this puzzle, we need to take into consideration keeping that $47,600 conservatively invested until death. Would we be able to draw $292/month from that balance?
Calculating savings drawdown
Bankrate has a great savings drawdown calculator that makes the math here clear and simple, along with a lovely chart:
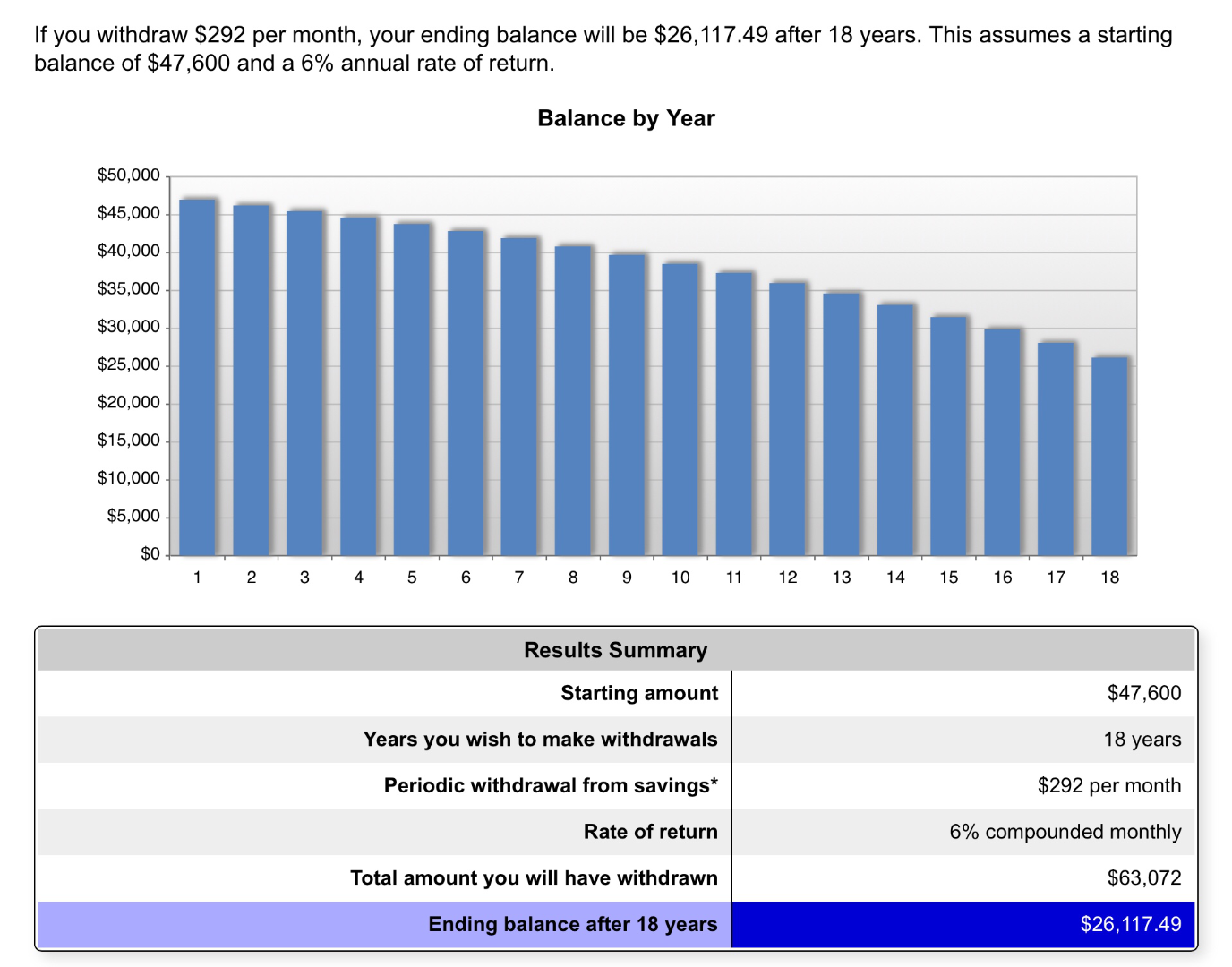
Finally, we’ve identified the necessary steps to effectively beat the SSA at the investment and actuarial game. Using the SSA’s example benefit data, my dad would kick the bucket with an extra $26K to his name by following the steps outlined above instead of waiting until age 66.8 to start drawing social security.
This is what he’d need to do:
- Start drawing from Social Security at the earliest age (62)
- Save the benefit ($708/month) and purchase conservative investments (with expected returns of 6%)
- At age 66.8, start drawing the benefit he would have earned at full retirement from his investment ($1,000/month)
- Keep the balance invested in conservative assets
While there’s certainly value in doing all of this, it’s actually more difficult to beat the SSA benefit increases as you age than I’d expected.
Retiring at 62: Pros and Cons
Making the decision between officially retiring with social security at age 62 or another older age shouldn’t be taken lightly. Planning ahead and making the decision based on your retirement goals and health will help you make the smartest financial decision.
Let’s review the upside to starting early.
Overall, there are many pros to drawing from social security at the youngest age and investing.
- Earlier access to funds can serve as an emergency fund
- Greater flexibility with investments mean higher potential upside value
- Likely greater asset value in your later years which could offer more flexibility and comfort at end of life
- Drawing down funds earlier from the SSA removes some risk of the SSA going belly up or changes to the law removing/reducing your access to benefits
- Lower annual benefit amounts yield lower total taxable income which might make the difference between qualifying for certain programs or not
- Lower benefit amounts also mean lower income thresholds for lower taxes on social security income itself
Of course, there are plenty of cons as we’ve discussed.
- More active approach, requiring more effort and interest in maintaining investments and managing withdrawals
- Assets are at greater risk—invested cash could follow the market down in a recession or depression even when invested conservatively
- Loss of the security the SSA offers when managing the funds
- Potential tax consequences of investment gains
- Potential social program qualification loss due to investment gains/income
- Greater annual benefit amounts could push recipients into higher income tax brackets, out of social security income specific deduction thresholds, or out of certain social programs that have income requirements
And these are just some of the retiring at 62 pros and cons we’ve worked through in this post.
Keeping tabs on your expected social security benefit and planning ahead will go far in maximizing the value of this government-run income insurance plan. Depending on your income situation in your 60s, deciding to draw your benefit at the earliest age could be smart if you plan, prepare, and execute a sound financial strategy. This is doubly true in the context of how it might affect your taxes.
So far as my father and his plans, I’m delivering the research I’ve done to help him make a decision. I don’t think it’s a very clear cut decision either way, and it’ll likely affect what decision my mother makes as well. She’s a bit younger than him, but is reaching the age 62 threshold.
What I’d most like to convey is that financially it seems like a bit of a toss-up in the big picture. What I want to discourage is them working longer partly to increase their social security benefit. I think they believe they have enough.
If you’re thinking about taking social security at 62, I hope this has been a productive review of the pros and cons. For readers closer to my own age, I don’t think it’s smart to not plan in advance for these sorts of decisions. While I suspect the age threshold will increase (or benefit gap at the lowest age increase), it’s still only about 25 years away for me. That’s not all that long!
Let me know in the comments if you’ve decided what age to starting drawing from social security. If you already are, tell me how you came to the decision to start if it was prior to age 70. Many of our readers are outside of the US, and I know there are similar programs to social security around the world. Tell us how yours works differently and about its own idiosyncrasies!


19 replies on “The Case for Taking Social Security at 62 (Pros and Cons)”
Other factors important to my decision when to start collecting SS:
1. Delaying drawing SS is “free” insurance against living to be very old. What if I live to be 100?
2. Delaying drawing SS increases the number of low earning years between starting retirement (say age 55) and collecting SS which can be used to fully convert traditional 401k/IRA funds to Roth and thus reduce income (and tax) whike drawing SS.
Great points, Michael! Thanks for coming by!
1) That’s a really solid point. While it’s ameliorated a little by cutting it the other way (what if you wait until 70 and die at 71), the range is pretty wide in the opposite direction. You could live a lot longer than you expect and draw on the higher retirement amount for a longer period of time that would eventually beat out investing + drawing earlier.
2) That Roth IRA conversion ladder angle isn’t one I thought of. Certainly a benefit. Our personal assets are pretty split (taxable/tax advantaged) so it’s mostly irrelevant to us and hence an oversight. Great point that you can have more years converting if that’s something you need!
My wife and I are basically your parents, age wise. However I paid the maximum into Social Security for every year I worked and I worked more years that Social Security requires to get the maximum benefit. I retired at the age of 60 and my wife has been a stay at home homemaker for the last thirty years. We retired with ample investments so that Social Security is merely more money to hand down to our grown kids someday. But the decision still had to be made when to take it. My wife’s Social Security for the nine years she did work outside the home is $950 a month. She’s taking that now. My Social Security we are delaying to age 70 when it will be $4,586 per month. At that time she will be able to switch to a spousal benefit of $1,755 for a total benefit for the two of us of $6,341 or somewhere over $70,000 a year. We may be constrained to the maximum Social Security allows a single family which is estimated to be about $73K in five years even though we are entitled to $76,000 according to their formulas. My reason for opting for age 70 is that when I die my wife will automatically assume my benefit instead of the much smaller spousal benefit. While my life expectancy is probably normal my wife still runs (and still wins) full marathons at age 66. I think she’ll blow past 100 with ease and the larger benefit I gained by waiting will slay anything I could have gotten by investing the money between age 66 and 70. And if it doesn’t it will still be a larger monthly check that will ease her mind even if she has millions she doesn’t need. All the numbers are approximate based on what Social Security tells me I have coming, since they estimate everything current dollars you have to guess about inflation to come up with how delayed benefits might increase.
Hey Steveark! Nice to see you around again. 🙂
As an aside, did that factor into your continuing to work decision at all? In other words, once you reached the 35-year max, did you think to yourself at all—”hm, I’ve put in the max amount for SS averaging, perhaps I don’t need to keep working”? One of the things my parents mention when I prod them is the idea of replacing lower-income years (since they’re already at the 35 year cap, too) with higher-income years to bump their SS benefits.
Phew, that’s a lot of money really! 🙂
If you can make some predictions like this, I think that’s a really smart and objective way to make the decision. Of course, anything can happen, but if you’ve got a solid reason to think you’ll under— or over-perform the actuarial tables, it makes sense to take advantage of either direction.
—
In general, as is probably clear from my first question in this comment, I’m wondering how much social security played into your quitting work decision-making. Of course, it affects your financial plans, but I feel like it’s odd to base when you’ll make a jump to a different type of life around hitting SS thresholds, maxing out the contribution, etc.
Thanks, as always, for your POV Steveark!
My heirs can’t inherit my SS. Could be a reason to take it early?
Hey Glincoln! I had to look into this a little more to understand the details…
It seems that your “heirs” (generically speaking), can indeed inherit your social security benefits. Spouse, kids, and even grandchildren, stepchildren, or adopted children.
https://www.ssa.gov/benefits/survivors/
That said, the intention seems to be for dependents. Your 45 year old son who works full-time isn’t going to start receiving your benefits unless under very specific circumstances or an unusual case.
Overall, I think you’re right though—if you’d like to leave your estate to your adult, working heirs—you might be able to increase the size of that estate by taking social security earlier and gifting more to them along the way.
Nice analysis, Chris. One other thing to be careful about when taking Social Security early (before 67, for those born after 1960), is that if you do happen to earn income in a year when you are 62 to 66, your Social Security benefit will be reduced by $1 for every $2 dollars over $18,960 you earn. Even for “retired” folks, a consulting gig or special project can come up, and that can end up wiping out some or even all of your Social Security income.
Keeping this in mind, when I run my numbers with my expected income profile, being careful to use 2021 dollars throughout, I’m better off filing at 62 if I live to at most 76, filing between 62 and 70 if I live to between 76-86, and filing at 70 if I live 86 or longer. Michael makes a great point that filing at 70 is a type of insurance to cover the situation if you happen to live really long.
Arman, great point! And I appreciate the age-based analysis.
I’m going to dig into the income related benefit deductions you mentioned. I ran across that in my research but mostly dismissed it, though I don’t recall why. I’d guess it’s unrelated to capital gains—and surely dividends wouldn’t trigger a cut. Off hand, I’d guess it’s only earnings that are also FICA taxed so W2 and possibly Self Employment/Schedule C. Probably not K-1 (partner) income which would be the long term concern for me. (I’m out enjoying the sun and river at the moment and will dig in later with a follow up).
Thanks for more pointed commentary Arman! Keep it coming. 🙂
Correct, capital gains and dividends will not trigger benefit reductions. Just salary.
There is another caution that is worth noting for the FIRE community: if you plan to retire before age 62, don’t take at face value the benefits estimates provided by the Social Security Administration for ages 62, 67, and 70. You will want to run the numbers yourself. This is because the SSA assumes your salary from now through your benefits filing year will be the same as your last year’s salary. For example, they will assume the great salary you earned last year will be earned every year through age 66, if you are filing at age 67. Of course this is wildly off for folks retiring early. Having less than 35 years of earnings history will proportionately cut into your average indexed monthly earnings (AIME), the key number used to compute the SS monthly benefit amount. I found it worthwhile to run a spreadsheet for retiring in year X and filing for SS in year Y, for all of the relevant X and Y.
Great points, again, Arman!
Yeah, you should definitely run the calculation yourself and be wary of the estimates. You can come up with an exact number given your existing history.
Does money you pull out of a 401K trigger a benefit reduction?
Add’l ‘case for 62’: today’s $s are worth more than tomorrow’s starting to take at 62 even at the discounted rate can be made up by the increased value of those $s in the 4 additional years you get the funds. Also, taking your SS early = not having to make like withdraws out of your retirement funds (and also having your taxes on them withheld up front) where you can be making additional profits that you wouldn’t have if you have to take out the funds. taking into consideration a modest inflation rate of 2-3 percent, and additional market returns of a modest 5-6 percent, for those add’l 4 years you supposedly are taking a cut on yuor benefits is not true at all – you end up at least the same or better. Not to mention if you are getting 2K a month – over 4.x years you’re 100k ahead than you would have been if you delayed til your FRA. Considering that you’re not going to actually be ‘taking a loss’ until you are in your early 80s at the earliest. If you have a financial advisor who just recites the usual mantra of waiting til FRA or 70, lay out this information and see what your advisor has to say. It’s just math. If he doesn’t understand it and/or if he doesn’t even want to consider it then it’s time to find another advisor.
Hey Dave!
Thanks for the additional perspective and tips! You’re right, I think I alluded to those points in the post—you can do better taking it early at 62 and investing while maximizing some of the other benefits. I think that, overall, the benefit ends up being a bit small (in absolute terms, dollar for dollar) while also taking a good bit more work and at least some risk that something happens in the market where you’re investing the funds you’ve taken out.
For lots of folks, I can see how that would make it not worth a bit of extra cash. But to your point, what really matters, is your own personal situation and running the numbers is what’ll get you to that decision point. Cheers!
I started drawing at my FRA of 66 and 2 months earlier this year. My wife is 61 and hasn’t worked for the last 3 years. She has worked enough to qualify for SS. I have a spreadsheet that runs out to 2026 which includes all of our current expenses as well as projected cost inflation, COLA adjustments and modest growth of our IRA. My spreadsheet assumes that she will start drawing at 62, so mid next year. While your analysis makes sense to me, my only concern is investing the SS difference until her FRA of 67. If we wait until her FRA, we would be required to draw from our IRA to cover our projected expenses. Hence, a delay will only draw down our savings by the same amount. I haven’t considered spousal benefits. My draw is approximately $1,900 per month higher than her draw at 62. What am I missing?
Hey Rick!
Thanks for the question and outline!
“If we wait until her FRA, we would be required to draw from our IRA to cover our projected expenses. Hence, a delay will only draw down our savings by the same amount”
The idea here is more that you can leverage the early withdraws (in your case, spend them) while keeping more money invested in your IRA. That only works if reality matches the assumption that your IRA will outperform the SS benefit growth over the same period. It *should*, but hey, markets are much less stable than a smooth and clearly defined SS growth curve.
The other option would be, to your point, keep her SS going until FRA and drawdown your IRA in the meantime to cover living expenses. That’s a bet that SS growth will beat your IRA’s investment performance.
Does that help it make more sense?
Thanks for the clarification. I surmised from your response that it’s better to wait until her FRA given a “guaranteed” rate of return versus an uncertain one from IRA investments. Makes perfect sense.
That’s certainly a reasonable way to look at it, Rick! It’s hard to predict which way the market will go, but SS should be safer. It really depends on your goals/needs and if SS will fill that role well enough. Cheers!
Here is a question I have, it is about spousal Social Security, when should my wife tax her Social security, should she take it early knowing that once I am gone she will get only half of my Social security! So will her waiting matter?
Hey Michael!
That’s a good question. My understanding is that spousal social security benefits and your own individual benefits are treated with separate “windows”.
This Q&A on USA Today seems to address your question directly.
TL;DR: it seems it shouldn’t matter.